【解析几何】准线与焦点
在学习圆锥曲线的过程中,我们必然会遇到诸多有关焦点这个特殊点的题目。比如下面这道:
设F1,F2分别为椭圆3x2+y2=1的左、右焦点,点A,B在椭圆上,若F1A=5F2B,则点A的坐标是()
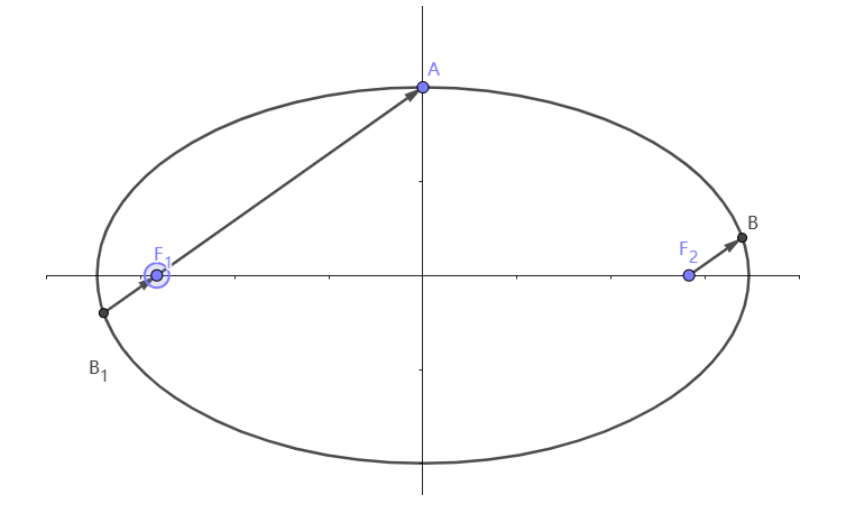
看到这里,很多同学可能就会选择联立求解,如下。
解法一:
由于对称性将F2B平移到左焦点,设A(x1,y1),B(x2,y2)由于直线AB1过左焦点,故设直线AB1:x=my−2.联立{x=my−2x2+3y2=3⟹(my−2)2+3y2=3
则⎩⎪⎪⎨⎪⎪⎧y1=−5y2y1+y2=−m2+322my1y2=−m2+11⇒{y1=−2(m2+3)my2=2(m2+3)5m⇒2(m2+3)5m2=1⇒m=±2所以点A(0,±1)
在这里看起来很简单,但计算量还是不小的。
考虑到 AB1 是椭圆的焦点弦,我们可以利用焦半径公式。这里就不得不提到圆锥曲线的统一定义了。
圆锥曲线的统一定义:到定点 F 的距离与到定直线 l 的距离(F 不在 l 上)的比 e 是常数的点的轨迹叫作圆锥曲线。
如图,椭圆a2x2+b2y2=1,F1,F2为其左右焦点,直线l:x=−ca2为其左准线,AC⊥l,则有∣AF1∣=e∣AC∣
实际上这也很好“证明”(证明一个“定义”有种儿子生爸爸矛盾了)
设点A(x0,y0),则∣AF1∣=(x0+c)2+y02=(1−a2b2)x02+2cx0+c2+b2=a1c2x02+2ca2x0+a4=a1(cx0+a2)=a+ex0而∣AC∣=x0+ca2=eex0+a=e∣AF1∣
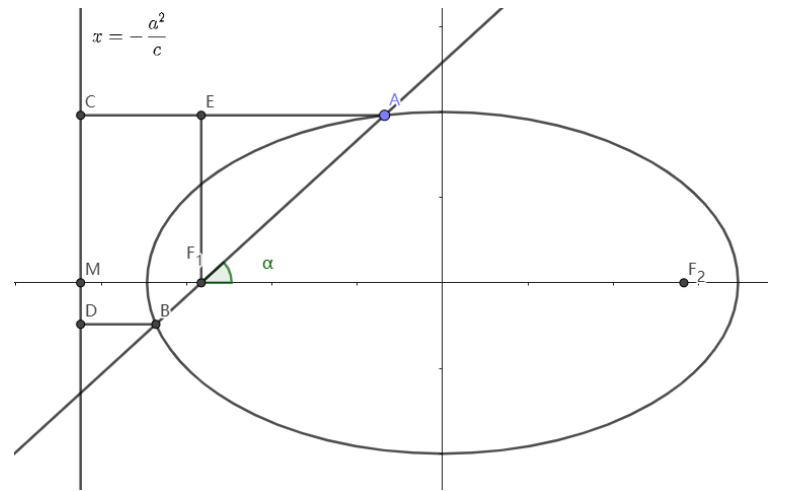
一般来说课本内容或一些资料就到此为止了,而我们学习抛物线时会有这么一个结论:
AB是过抛物线y2=2px的一条直线,F为抛物线焦点,A在x轴上方,θ为直线AB的倾斜角,则有∣AF∣=1−cosθp,∣BF∣=1+cosθp∣AB∣=sin2θ2p,∣AF∣1+∣BF∣1=p2
那么是不是所有圆锥曲线都有类似性质呢,根据圆锥曲线统一定义我们推断这肯定是存在的。
如上图,对于一个椭圆,设AB的倾斜角为α,∣AF1∣=m,则∣AE∣=mcosα∣AC∣=ca2−c+mcosα=cam⟹m=a−ccosαb2,即∣AF1∣=a−ccosαb2同理可得∣BF1∣=a+ccosαb2∣AB∣=a2−c2cos2α2ab,∣AF1∣1+∣BF1∣1=b22a同理,对于双曲线a2x2−b2y2=1,过其左焦点F的直线AB,有∣AF∣=a+ccosαb2,∣BF∣=a−ccosαb2,∣AB∣=a2−c2cos2α2ab,∣AF1∣1+∣BF1∣1=b22a注意AB交于双曲线左支,所以∣cosα∣≤ca
利用该结论,再看上面那道题:
设F1,F2分别为椭圆3x2+y2=1的左、右焦点,点A,B在椭圆上,若F1A=5F2B,则点A的坐标是()
解法二:
∣F1A∣=5∣F1B1∣⟹3−2cosθ1=3+2cosθ5⟹cosθ=36=ac∴A(0,±1)
这样计算甚至降到了口算量级,下面我们再来看这样一道题。
设点P为椭圆C:6x2+2y2=1上任意一点,过两焦点F1,F2的弦分别为PA,PB,设PF1=λ1F1A,PF2=λ2F2B,问λ1+λ2是否是定值,并证明
这里我们直接利用焦点弦结论
∵∣AF1∣1+∣PF1∣1=∣PF1∣1+λ1=b22a=6,∣AF2∣1+∣PF2∣1=∣PF2∣1+λ2=b22a=6∴6(∣PF1∣+∣PF2∣)=2+λ1+λ2=2×6=12∴λ1+λ2=10
几乎是“秒杀”,那么我们来看一道高考题。
已知椭圆3x2+2y2=1的左右焦点分别为F1,F2,过点F1的直线交椭圆于B,D两点,过点F2的直线交椭圆于A,C两点,且AC⊥BD,垂足为P,求四边形ABCD的面积最小值。
设AC,BD的倾斜角分别为α,β,看到垂直的条件,我们不妨设α=β+2π那么cosα=−sinβ所以S=21∣AC∣∣BD∣=(a2−c2cos2β)(a2−c2sin2β)2a2b4=6+41sin22β24≤2596
此外利用好点到焦点焦点和点到准线还能处理一些角的问题,如下。
已知抛物线y2=2px(p>0)的焦点为F,准线为l,l与x轴交点为M,过点F的直线AB交抛物线于AB两点A在x轴上方,∠AMB=3π,∣AF∣=2+3,试求抛物线方程.
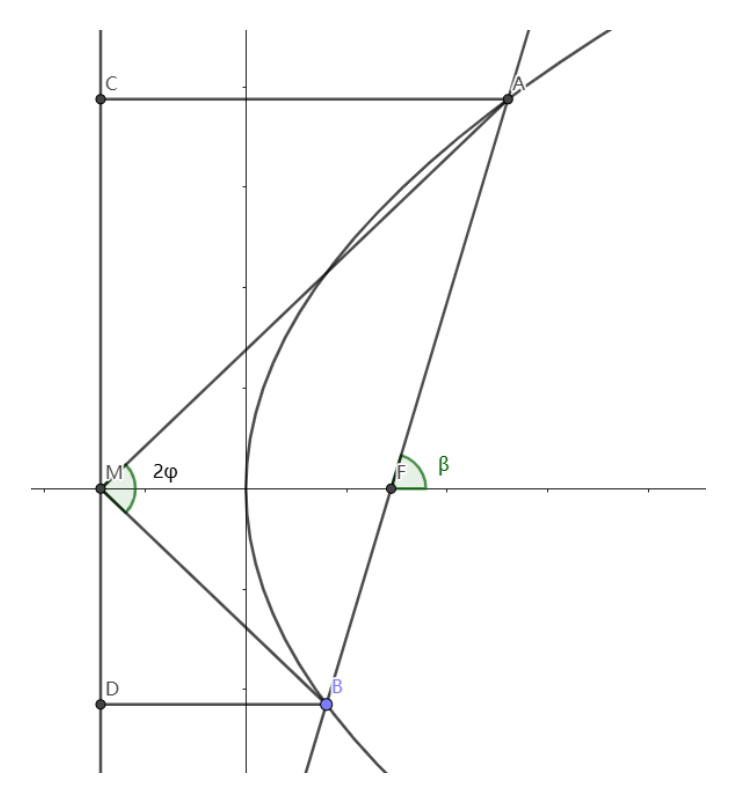
如图设∠AMF=φ,直线AB的倾斜角为β,则有sinβ=AFCM=ACCM=tanφ同理sinβ=tan∠BMF,所以∠AMF=∠BMF∴sinβ=33,∣AF∣=1−cosβp=2+3解得:p=33,所以抛物线方程为:y2=323x
同样椭圆双曲线也有类似结论,证明也很简单,大家不妨自行尝试推导。
在圆锥曲线部分,有关焦点的问题可以说是俯拾即是,利用上述结论可以迅速解决大部分这类问题,节省大量时间,但同时不要忘记对于基础联立韦达的解法对一般情况进行求解,否则遇到非焦点问题可就是“提笔四顾心茫然”,感谢您的阅读,希望这篇文章能够帮助到你。
本文作者:Rhonsua
本文链接:https://yurchiu.github.io/2024/08/06/%E3%80%90%E8%A7%A3%E6%9E%90%E5%87%A0%E4%BD%95%E3%80%91%E5%87%86%E7%BA%BF%E4%B8%8E%E7%84%A6%E7%82%B9/
版权声明:本博客中所有原创文章除特别声明外,均允许规范转载,转载请注明出处。所有非原创文章,按照原作者要求转载。
浏览量:
最后更新:2024-08-06, 19:16:50




